2021-04-24

tf.keras概述

tf.keras概述

使用tf.keras实现一个简单的线性回归

建立一个受教育年限和收入的线性预测模型

import tensorflow as tf
import pandas as pd 
import matplotlib.pyplot as plt
# 在jupyter notebook中使用,使结果直接输出在控制台中 
%matplotlib inline
print(tf.__version__)
# 读取数据
data = pd.read_csv('Income1.csv')
data
# 绘制散点图
plt.scatter(data.Education,data.Income)
# 定义维度
x = data.Education 
y = data.Income
# 建立线性模型
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(1,input_shape=(1,)))
# 打印模型信息
model.summary()
# 定义优化器和损失函数
model.compile(
    optimizer='adam',
    loss='mse'
)
history = model.fit(x,y,epochs=5000)
# 使用模型预测
model.predict(pd.Series([8]))

梯度下降算法

梯度下降算法是一种致力于找到函数极值点的算法。

梯度的输出是一个由若干偏导数构成的向量,他的每个分量对应于函数对输入向量的相应分量的偏导。

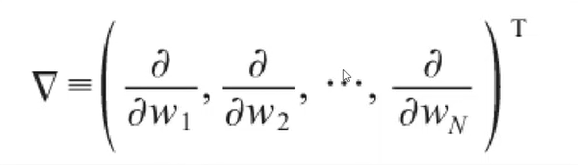
梯度的输出向量表明了在每个位置损失函数增长的最快的方向,可将它视为表示了在函数的每个位置向哪个方向移动函数值可以增长。

多层感知器

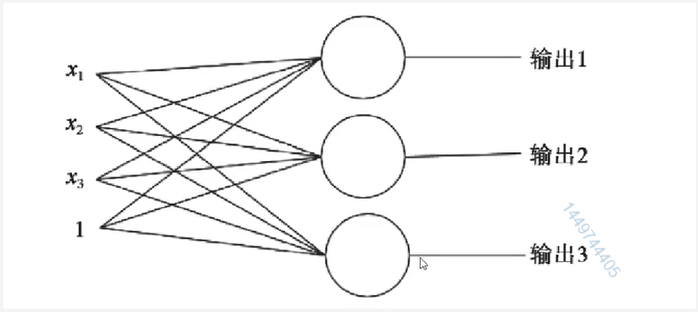
单层神经元的缺陷

神经元要求数据必须是线性可分的
异或问题无法找到一条直线分割两个类。

多层神经元

生物的神经元一层一层连接起来,当神经信号达到某一个条件,这个神经元就会激活,然后继续传递信息下去。
为了继续使用神经网络解决这种不具备线性可分性的问题,采取在神经网络的输入端和输出端之间插入更多的神经元

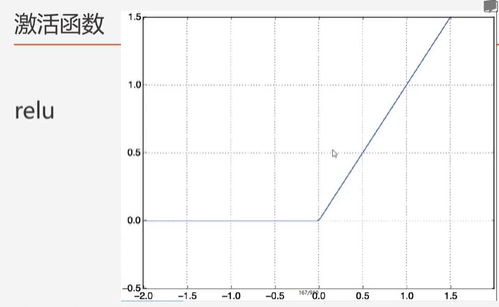
relu激活函数

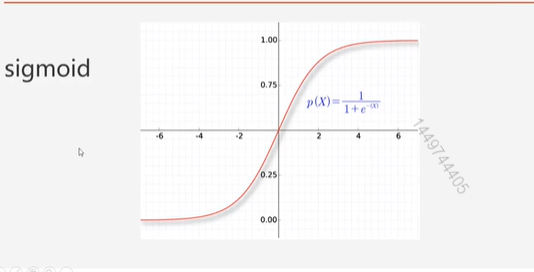
sigmoid激活函数

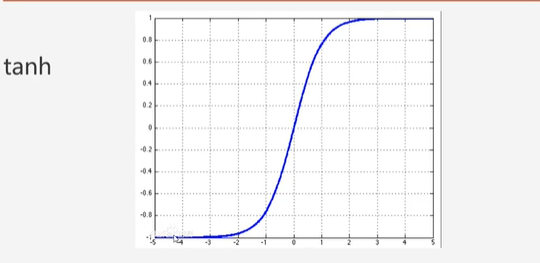
tanh激活函数

使用tf.keras实现一个简单的逻辑回归

import tensorflow as tf
import pandas as pd 
import matplotlib.pyplot as plt
# 在jupyter notebook中使用,使结果直接输出在控制台中 
%matplotlib inline
data = pd.read_csv('credit-a.csv',header=None)
# 定义维度
x = data.iloc[:, :-1]
y = data.iloc[:, -1].replace(-1,0)
x
# 创建模型
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(100, input_shape=(15,),activation='relu'))
model.add(tf.keras.layers.Dense(100, activation='relu'))
model.add(tf.keras.layers.Dense(1, activation='sigmoid'))
model.compile(
    optimizer='adam',
    loss='binary_crossentropy',
    metrics=['acc']
)
history = model.fit(x,y,epochs=1000)
model.predict(data.iloc[:20, :-1])
plt.plot(history.epoch,history.history.get('acc'))